A 建立火车站
题目描述
新冠疫情,导致了各个城市之间物资输送的障碍。假设有N个城市在一条直线上,为了物资能顺利抵达各个城市,可以在路线上建立最多个数为K个暂时停靠站,由于火车在两个站台(城市也算站台)之间的距离越近,需要的总花费越少,因此我们需要让火车相邻两个站台之间的最大距离最小,求出距离L,2 ≤N ≤100000, 0 ≤K ≤100000,所有城市坐标小于等于10^12,且不存在负值。提醒: 城市坐标均为正整数,且停靠站只能建在整数坐标点上。
输入描述
第一行输入城市个数N,可建立停靠站个数K, 第二行输入N个城市的坐标(不保证前一个城市坐标比后一个城市小)。
输出描述
输出L
样例输入
2 2
4 106样例输出
34java代码:
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
long[] city = new long[n];
for(int i=0;i<n;i++)
city[i] = scanner.nextLong();
Arrays.sort(city);//排序
long[] dis = new long[n-1];
for(int i=0;i<n-1;i++)
dis[i] = city[i+1]-city[i];//相邻两城市之间的距离
long l = 1;
long r = (long)10e13;
while(l<=r)
{
//右移运算
long mid = (l+r)>>1;
long c = 0;
for(int i=0;i<n-1;i++)
c+=(long)Math.ceil(dis[i]*1.0/mid)-1;//向上取整
if(c>k)l = mid+1;
else r = mid-1;
}
System.out.println(l);
}
}B cyj真的不是0(easy version)
题目描述
从开营以来,总有人天天叫池学姐(我不说是谁^___^),并让可爱的cyj学长女装,cyj觉得自己不是0,但总被人叫学姐(啊啊啊啊啊啊),因此,cyj觉得自己必须是1才能摆脱大家的嘲讽。 但是,cyj每天都会收到大家的嘲讽诸如000,00 ,01010100011这样的字符串,因此,cyj想出了这样一个问题,如果给定2n个数,其中只有n个0和n个1,他们按照某种顺序排成长度2n的序列,其中满足任意前缀序0的个数都不少于1的个数的序列的数量是多少?,cyj忙于和他们对线,因此把问题交给了你,你能帮忙回答他吗
输入描述
输入一个正整数n,1<=n<=6
**输出描述
输出一个正整数,结尾没有空行
样例输入
3样例输出
5java代码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n=scanner.nextInt();
int s1=2*n;
int s2=n;
int sum1=s1;
int sum2=s2;
while(s1--!=n+1)
{
sum1 *= s1;
}
while(s2--!=1)
{
sum2 *= s2;
}
int res=(sum1/sum2)/(n+1);
System.out.println(res);
}
}C 辛苦出题的翰翰
题目描述
这天,xzh在出题过程中遇到了瓶颈,才思枯萎,特地上某个小破站找找灵感,增加知识储备。于是,他在科普区(搞笑区)看见了这个:
渣篮,一种用牙签制作成的篮子,因为是用牙签做成的,所以渣篮的体积非常小,如果说它哪里比较大,应该也只有它产自加拿大。众所周知,木制品是绝缘体,所以用牙签做成的渣篮一般是用来装电鳗这种废物(比较费钱的生物),电鳗在渣篮里会不停的运动,在这个过程中,渣篮里的牙签会越来越细,“鳗功出细活”指的就是这么一种现象…
一不小心普及的有点多,让我们回归到渣篮的本质,就是小,那么问题来了,先输入n,代表n个数,再输入n个数,找到最渣篮,即为最小的那个数,并输出。
输入描述
先输入n,再输入n个数。
输出描述
输出n个数当中最小的那个。
样例输入
3
1 2 3样例输出
1java代码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n =scanner.nextInt();//输入的行数
int []a = new int [100000];
for(int i=0;i<n;i++) {
a[i]=scanner.nextInt();
}
int min=a[0];
for(int i=0;i<n;i++) {
if (min>a[i]) {
min=a[i];
}
}
System.out.println(min);
}
}D 群宝的考验
题目描述
导数是数学中的重要工具,在高数里对导数的定义做了详细的概述,导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f’(x0)或df(x0)/dx。
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f’(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。反之,已知导函数也可以反过来求原来的函数,即不定积分。
微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作,它们都是微积分学中最为基础的概念。
在高数中有很多求导的题目。群宝深知代码改变生活的道理,所以希望有一个可以有一个求导的程序来帮助他,需要你来写一个可以实现自动求导的程序,通过群宝的考验,将会获得来自群宝的神秘大奖嗷。
为了简化这个问题,我们只研究对幂函数求导。我们将给出幂函数的幂次n和求导次数k,要求你输出幂函数在经历k次求导后的幂次;
输入描述
程序将输入两个整数n,k,用空格隔开分别代表函数的幂次以及求导的次数。(-1e9≤n≤1e9; 0≤k≤1e9)题目保证输入输出都在int型范围内。
输出描述
输出一个整数,表示函数求导后的的幂次。
样例输入
10 3样例输出
7java代码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
System.out.println(n-k);
}
}F 溜圈圈
题目描述
BigSheep总是喜欢溜圈,但是他有几个原则:
- 只能向左转,且不能在同一个地方多次左转。
- 每次只走不同的圈。
- 每次走圈走遍整个区域,同一个点只去一次,起点不一定需要等于终点。
有一天,BigSheep半夜睡不着觉,跑去操场溜圈。我们可以认为操场是一个n×m的网格图,神奇的BigSheep可以把任意一个格子当作自己的起点开始绕圈,对于BigSheep那些奇怪的原则,我们可以抽象成以下几点:
- BigSheep在起点时可以任意选择自己的朝向。
- 每次只能直走,或者左转后直走,且不能越过边界。
- 每次走圈的路径不能一样,即同一个路径不能走多次(对于两条路径,存在一个格子(x_0,y_0)(x0,y0)在第一条路径中是第ii个访问的,在第二条路径中是第jj个访问的,且i\not= ji̸=j,我们即可认为这两条路径是不同的)。
- 每次溜圈都需要遍历每一个格子,且每一个格子只能被访问一次,溜圈的起点和终点不需要保证相邻。
BigSheep想知道自己最多可以溜多少圈。
样例输入
1
2 2
样例输出
4
样例解释:
所以四种方案如下:
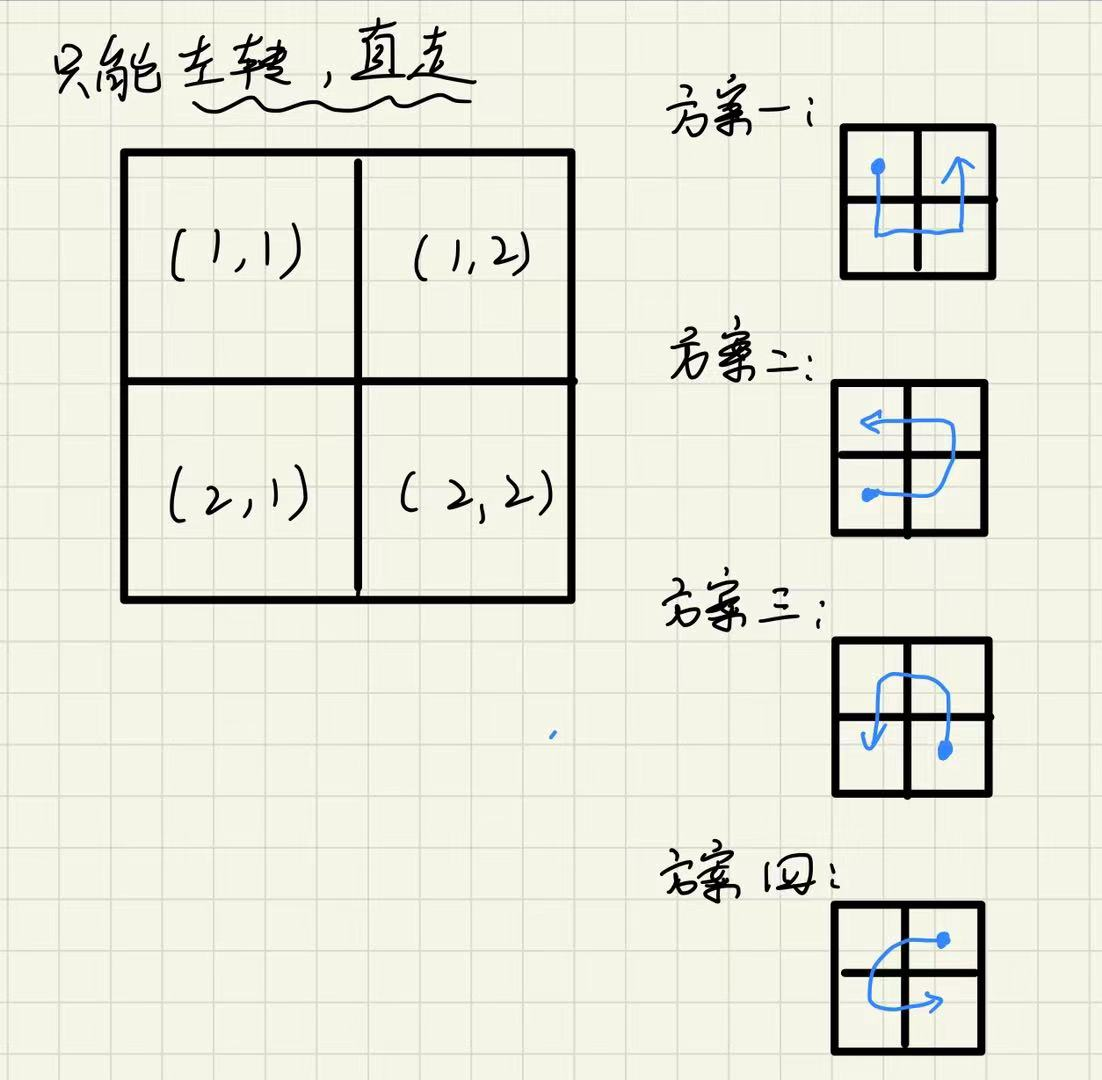
输入描述
先输入一个T(1≤T≤1000)表示测试数据组数。
接着每一行输入两个整数n,m(1≤n,m*≤1000),分别表示操场的长和宽。
输出描述
输出共T*T行,每行表示一组测试数据的答案。
java代码:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int T = scanner.nextInt();
while(T--!=0) {
int m =scanner.nextInt();
int n =scanner.nextInt();
if (m>=n) {
int temp = m;
m=n;
n=temp;
}
if (m==1 && n==1) {
System.out.println(1);
}
else if (m==1 && n>1) {
System.out.println(2);
}else if (m>1 &&n>1) {
System.out.println(2*(m + n -2));
}
}
}
}